



Next: Revised definition of general
Up: Point-to-Point Communication
Previous: Null processes
Contents
Derived datatypes
In C or Fortran bindings of MPI, derived datatypes have two roles.
One is to allow messages to contain mixed types (for example they
allow an integer count followed by a sequence of real numbers to be
passed in a single message). The other is to allow noncontiguous data
to be transmitted.
In mpiJava the first role is abandoned.
Any derived type can only include elements of a single basic type.
- Rationale. In the C binding of MPI, for example, the MPI_TYPE_STRUCT
constructor for derived types might be used to describe the physical
layout of a struct containing mixed types. This will not
work in Java, because Java does not expose the low-level layout of its
objects. In C and Fortran another use of MPI_TYPE_STRUCT
involves incorporating offsets computed as differences between absolute
addresses, so that parts of a message can come from separately declared
entities. It might be possible to contrive something analogous in a Java
binding, somehow encoding object references instead of physical
addresses. Such a contrivance is unlikely to be
very natural--even in C and Fortran the mechanism is not
particularly elegant.
Meanwhile, the effect of either of these applications of
MPI_TYPE_STRUCT can be achieved by using MPI.OBJECT
as the buffer type, and relying on Java object serialization.(End of rationale.)
This leaves description of noncontiguous buffers as the
essential role for derived data types in mpiJava.
Every derived data type constructable in mpiJava has
a uniquely defined base type. This is one of the 9 basic
types enumerated in section 3.2.
Derived types inherit their base types from their precursors in
a straightforward way.
In mpiJava a general datatype is an object that
specifies two things
- A base type
- A sequence of integer displacements
In contrast to the C and Fortran bindings the displacements are
in terms of subscripts in the buffer array argument, not
byte displacements.
The base types for the predefined MPI datatypes are
| MPI datatype |
base type |
| MPI.BYTE |
byte |
| MPI.CHAR |
char |
| MPI.SHORT |
short |
| MPI.BOOLEAN |
boolean |
| MPI.INT |
int |
| MPI.LONG |
long |
| MPI.FLOAT |
float |
| MPI.DOUBLE |
double |
| MPI.OBJECT |
Object |
| MPI.LB |
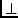 |
| MPI.UB |
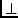 |
| MPI.PACKED |
byte |
The symbol 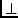 is a special undefined value.
The displacement sequences for the predefined types (other than
MPI.LB, MPI.UB) consist of a single zero.
is a special undefined value.
The displacement sequences for the predefined types (other than
MPI.LB, MPI.UB) consist of a single zero.
If the displacement sequence of a datatype is
we define
- Rationale. This definition of the extent differs from the definition in the C or
Fortran. It is in units of the buffer array index, not in units
of bytes.(End of rationale.)
As discussed at the end of this section, these definitions have to be
modified if the type construction involves MPI.LB, MPI.UB.
static Datatype Datatype.Contiguous(int count, Datatype oldtype)
| count |
replication count |
| oldtype |
old datatype |
| |
|
| returns: |
new datatype |
Construct new datatype representing replication of the old datatype into
contiguous locations.
Java binding of the MPI operation MPI_TYPE_CONTIGUOUS.
The base type of the new datatype is the same as the base type of
the old type. Assume the displacement sequence of the old type is
with extent ex. Then the new datatype has a displacement sequence
with count  n entries defined by:
n entries defined by:
static Datatype Datatype.Vector(int count,
int blocklength, int stride,
Datatype oldtype)
| count |
number of blocks |
| blocklength |
number of elements in each block |
| stride |
number of elements between start of each block |
| oldtype |
old datatype |
| |
|
| returns: |
new datatype |
Construct new datatype representing replication of the old datatype into
locations that consist of equally spaced blocks.
Java binding of the MPI operation MPI_TYPE_VECTOR.
The base type of the new datatype is the same as the base type of
the old type. Assume the displacement sequence of the old type is
with extent ex. Let bl be blocklength.
Then the new datatype has a displacement sequence
with count 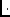 bl
bl 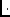 n entries defined by:
n entries defined by:
static Datatype Datatype.Hvector(int count,
int blocklength, int stride,
Datatype oldtype)
| count |
number of blocks |
| blocklength |
number of elements in each block |
| stride |
number of elements between start of each block |
| oldtype |
old datatype |
| |
|
| returns: |
new datatype |
Identical to Vector except that the stride is expressed
directly in terms of the buffer index, rather than the units of the old type.
Java binding of the MPI operation MPI_TYPE_HVECTOR.
Unlike other language bindings, the value
of stride is not measured in bytes.
The displacement sequence of the new type is:
static Datatype Datatype.Indexed(int [] array_of_blocklengths,
int [] array_of_displacements,
Datatype oldtype)
| array_of_blocklengths |
number of elements per block |
| array_of_displacements |
displacement of each block in units of old type |
| oldtype |
old datatype |
| |
|
| returns: |
new datatype |
Construct new datatype representing replication of the old type into
a sequence of blocks where each block can contain a different number
of copies and have a different displacement.
Java binding of the MPI operation MPI_TYPE_INDEXED. The number
of blocks is taken to be size of the arrayOfBlocklengths
argument. The second argument, array_of_displacements, should
be the same size.
The base type of the new datatype is the same as the base type of
the old type. Assume the displacement sequence of the old type is
with extent ex. Let B be the array_of_blocklengths
argument and D be the array_of_displacements argument.
Then the new datatype has a displacement sequence with
![$n \cdot \sum_{i=0}^{\mbox{\em count} - 1} \mbox{\tt B}[i]$](img11.png) entries:
entries:
Here, count is the number of blocks.
static Datatype Datatype.Hindexed(int [] array_of_blocklengths,
int [] array_of_displacements,
Datatype oldtype)
| array_of_blocklengths |
number of elements per block |
| array_of_displacements |
displacement in buffer for each block |
| oldtype |
old datatype |
| |
|
| returns: |
new datatype |
Identical to indexed except that the displacements are expressed
directly in terms of the buffer index, rather than the units of the old type.
Java binding of the MPI operation MPI_TYPE_HINDEXED.
Unlike other language bindings, the values
in array_of_displacements are not measured in bytes.
The displacement sequence of the new type is:
static Datatype Datatype.Struct(int [] array_of_blocklengths,
int [] array_of_displacements,
Datatype [] array_of_types)
| array_of_blocklengths |
number of elements per block |
| array_of_displacements |
displacement in buffer for each block |
| array_of_types |
type of elements in each block |
| |
|
| returns: |
new datatype |
The most general type constructor.
Java binding of the MPI operation MPI_TYPE_STRUCT. The number
of blocks is taken to be size of the array_of_blocklengths
argument. The second and third arguments, array_of_displacements
and array_of_types, should be the same size.
Unlike other language bindings, the values
in array_of_displacements are not measured in bytes.
All elements of array_of_types with definite base types must have the
same base type: this will be the base type of new datatype.
Let T be the array_of_types argument.
Assume the displacement sequence of the old type
![$\mbox{\tt T}[i]$](img14.png) is
is
with extent
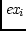 . Let B be the array_of_blocklengths
argument and D be the array_of_displacements argument.
Then the new datatype has a displacement sequence with
. Let B be the array_of_blocklengths
argument and D be the array_of_displacements argument.
Then the new datatype has a displacement sequence with
![$\sum_{i=0}^{c - 1} \mbox{\tt B}[i] \cdot n_i$](img17.png) entries:
entries:
Here, 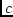 is the number of blocks.
is the number of blocks.
If any elements of array_of_types are MPI.LB or MPI.UB,
the corresponding displacements are omitted in the displacement
sequence. These displacements only affect the computation of
Datatype.Lb, Datatype.Ub and Datatype.Extent,
as explained below.
Subsections




Next: Revised definition of general
Up: Point-to-Point Communication
Previous: Null processes
Contents
Bryan Carpenter
2002-07-12
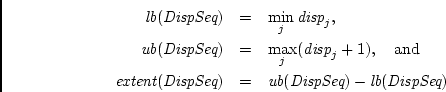
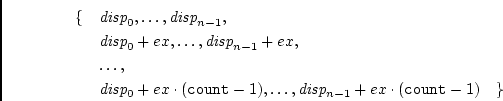


![\begin{eqnarray*}
&\{ & \mbox{\em disp}_0 + \mbox{\tt D}[0] \cdot \mbox{\em ex},...
...{\tt B} [\mbox{\em count} - 1] - 1) \cdot \mbox{\em ex}
\quad \}
\end{eqnarray*}](img12.png)
![\begin{eqnarray*}
&\{ & \mbox{\em disp}_0 + \mbox{\tt D}[0],
\ldots,
\mbox{\em...
...{\tt B} [\mbox{\em count} - 1] - 1) \cdot \mbox{\em ex}
\quad \}
\end{eqnarray*}](img13.png)
![\begin{eqnarray*}
&\{ & \mbox{\em disp}^0_0 + \mbox{\tt D}[0],
\ldots,
\mbox{\...
... (\mbox{\tt B} [c - 1] - 1) \cdot \mbox{\em ex}_{c - 1}
\quad \}
\end{eqnarray*}](img18.png)